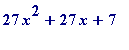 are precisely those primes
p
= 1 (mod 3) for which
are precisely those primes
p
= 1 (mod 3) for which
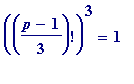 (mod
p
), the nagging question is:
what
determines the value of
(mod
p
), the nagging question is:
what
determines the value of
/3)!](images/reduced TCD talk 9th Feb 2005696.gif) ?
?
Main outstanding problem
Given that the prime values of the quadratic
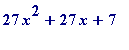 are precisely those primes
p
= 1 (mod 3) for which
are precisely those primes
p
= 1 (mod 3) for which
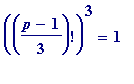 (mod
p
), the nagging question is:
what
determines the value of
(mod
p
), the nagging question is:
what
determines the value of
/3)!](images/reduced TCD talk 9th Feb 2005696.gif) ?
?
In short, what makes such a prime p be in the (earlier) sequence
3571, 4219, 13669, 25117, 55897, 89269, 102121, 170647, � (2)
rather than in the (earlier) sequence
7, 61, 331, 547, 1951, 2437, 7351, 8269, 9241, 10267, 23497, � (4)